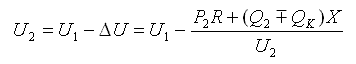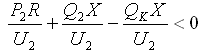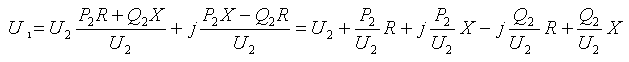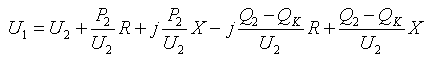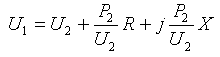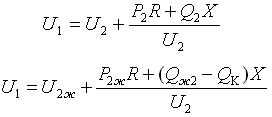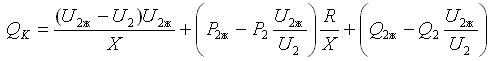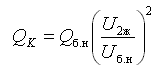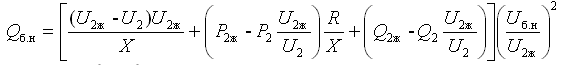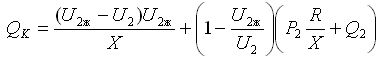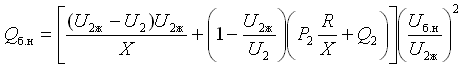Регулирование напряжения изменением реактивной мощности

 Сущность регулирования напряжения за счет воздействия на потоки реактивной мощности по элементам электрической сети заключается в том, что при изменении реактивной мощности изменяются потери напряжения в реактивных Сопротивлениях. Так, для схемы сети, приведенной на рис. 1, связь между напряжениями начала U₁, и конца U₂ можно записать в виде:

(1)

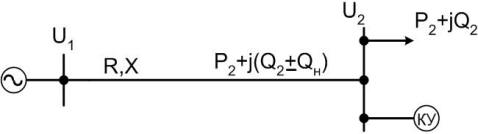
Рис. 1 Схема сети с компенсирующим устройством

В отличие от активной мощности, реактивную мощность в узлах сети можно изменять путем установки в них устройств поперечной компенсации, т. е. компенсирующих устройств (КУ), подключенных параллельно нагрузке. В качестве таких компенсирующих реактивную мощность устройств могут служить батареи конденсаторов, синхронные компенсаторы, шунтирующие и управляемые реакторы, статические тиристорные компенсаторы. К таким устройствам могут быть также отнесены генераторы местных электростанций, подключенных к системе передачи и распределения электроэнергии, синхронные электродвигатели, фильтры высших гармоник. Часть из указанных компенсирующих устройств может только выдавать в сеть реактивную мощность, некоторые - только потреблять из сети реактивную мощность (шунтирующие и управляемые реакторы). Наиболее ценными для регулирования напряжения являются устройства, обладающие способностями в зависимости от режима сети как генерировать, так и поглощать реактивную мощность (синхронные компенсаторы, статические тиристорные компенсаторы).

Компенсирующие устройства могут быть нерегулируемыми и регулируемыми. При включении нерегулируемого компенсирующего устройства в сети создается постоянная добавка потери напряжения (отрицательная или положительная). Если же компенсирующее устройство позволяет изменить свою мощность в зависимости от режима сети, то добавка потери напряжения, как это следует из формулы (1), оказывается переменной, в результате чего появляется возможность регулировать напряжение. Так, в схеме сети, приведенной на рис. 1, при изменении компенсирующим устройством мощности Q_K от выдачи (знак «минус» в формуле (1) перед Q_K) до потребления (знак «плюс» перед Q_K) будет изменяться потеря напряжения, что при неизменном напряжении U₁ = const приведет также к изменению напряжения U₂ в конце сети, т. е. будет обеспечено регулирование напряжения.

Как следует из формулы (1), эффективность регулирования напряжения с помощью поперечных компенсирующих устройств повышается в сетях с относительно большими" реактивными сопротивлениями по сравнению с активными, например, в воздушных сетях по сравнению с кабельными. При этом наибольший эффект достигается при установке компенсирующих устройств в наиболее удаленных от центров литания узлах нагрузки.

С помощью поперечного компенсирующего устройства можно создать режим, в котором напряжение в конце сети окажется больше напряжения в начале (U₂ > U₁). Это произойдет тогда, когда потеря напряжения в формуле (1) станет отрицательной:

Отсюда мощность компенсирующего устройства для такого режима

(2)

Физическую сущность регулирования напряжения с помощью поперечных компенсирующих устройств дополнительно поясним на векторных диаграммах. Для этого связь между напряжением U1 и U₂ запишем через падение напряжения:

(3)

При установке компенсирующего устройства, выдающего реактивную мощность,

(4)

Для случая, когда генерируемая мощность компенсирующего устройства полностью компенсирует реактивную нагрузку потребителей (Q_K = Q₂)

(5)

На рис. 2, а показана векторная диаграмма напряжений без компенсирующего устройства и с компенсирующим устройством при Q_K < Q₂, построенная по формулам (3) и (4). Здесь ∆U_a-падения напряжения от передачи активной мощности, a ∆U_p- реактивной мощности без компенсирующего устройства. Из диаграммы видно, что при установке компенсирующего устройства значение ∆U_a не изменяется, а вектор ∆U_p занимает положение ∆U_p.k. В результате исходный вектор напряжения ∆U₁ в начале линии уменьшается по модулю и становится равным ∆U_1k. Таким образом, для получения заданного напряжения U₂ за счет установки компенсирующего устройства потребуется меньшее напряжение ∆U₁ в результате снижения падения напряжения.

На рис. 2, б показан случай, когда полностью скомпенсирована реактивная мощность потребителей (Q_K = Q₂), в результате чего падение напряжения ∆U_p.k от передачи реактивной мощности полностью отсутствует (формула (5). И, наконец, на рис. 2, в показан исходный режим без компенсирующего устройства и режим, когда мощность компенсирующего устройства Q_K > Q₂ и удовлетворяет условию (2). В этом случае падение напряжения в активном и реактивном сопротивлениях изменяет знак, а напряжение U₂ становится больше U_1k.

Компенсирующие устройства поперечной компенсации оказывают комплексное положительное влияние на режим электрических сетей. Кроме возможности регулирования напряжения, они позволяют снизить потери активной мощности и электроэнергии за счет разгрузки элементов сети от реактивной мощности и соответственно снижения рабочих токов. В ряде случаев, когда передаваемая активная мощность ограничивается допустимым током по нагреванию или допустимой потерей напряжения, за счет разгрузки сети от реактивной мощности можно увеличить пропускную активную мощность. Поэтому в общем случае вопросы выбора мощности и мест установки компенсирующих устройств должны решаться комплексно. Здесь же, однако, рассмотрим подход к выбору мощности компенсирующего устройства по условию регулирования напряжения [3,16, 24].

Пусть при U₁=const напряжение U₂ по каким то причинам не удовлетворяет потребителей (рис. 1), и его надо повысить до U_2ж с помощью выбора соответствующей мощности компенсирующего устройства, устанавливаемого в конце сети При расчете в общем случае следует учесть, что при повышении напряжения U₂ до U_2ж произойдет изменение потребляемых нагрузок P₂ и Q₂ до P_2ж и U_2ж в соответствии с их статическими характеристиками P₂=f(U₂) и Q₂=f(U₂). Этот фактор может не учитываться в том случае, если нагрузка подключена на вторичной стороне трансформатора, имеющего устройство РПН, которое позволяет сохранить напряжение на шинах низшего напряжения неизменным.

До и после установки компенсирующего устройства мощностью Q_K связь между напряжениями начала и конца сети можно соответственно представить в виде:

Приравнивая правые части данных уравнений вследствие условия U₁=const, найдем мощность компенсирующего устройства

(6)

Здесь мощности P₂, Q₂, P_2ж, Q_2ж  находятся по соответствующим статическим характеристикам

Если в качестве компенсирующего устройства выступает батарея конденсаторов, то ее мощность зависит от подводимого напряжения:

где Q_б.н номинальная мощность батареи конденсаторов при номинальном напряжении U_б.н

С учетом этой зависимости номинальная мощность батареи конденсаторов для изменения напряжения U₂ до U_2ж должна быть равна

(7)

 

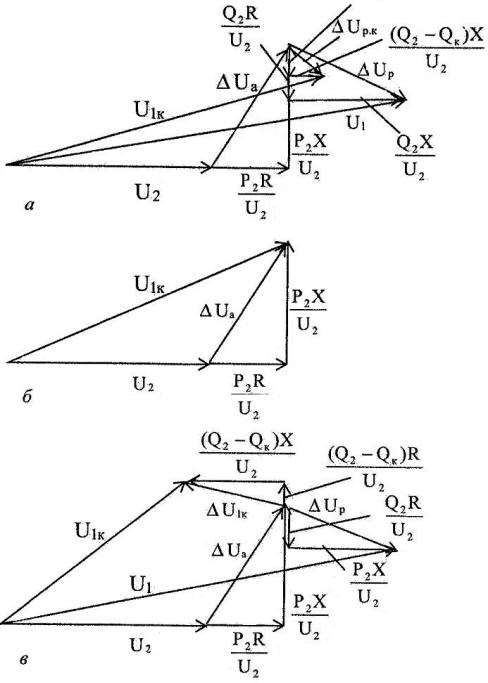
Рис. 2. Векторные диаграммы напряжений при выдаче реактивной мощности компенсирующим устройством: а - при Q_K < Q₂; 6 - при Q_K = Q₂; в - при Q_K > Q₂ и U₂ > U, С

В случае неучета статических характеристик нагрузки P_2ж=P₂ и Q_2ж=Q₂. Тогда необходимая мощность компенсирующего устройства из формулы (6) получается в виде:

(8)

Для компенсирующего устройства в виде батареи конденсаторов из формулы (7) соответственно получим:

(9)